مدارات ترکیبی (R & L & C)
- Morteza Aghajani
- دانشگاه
در این آموزش، مدارهایی را معرفی خواهیم کرد که از ترکیب دوتایی عناصر پسیو ساخته میشوند. این مدارها، مدار شامل مقاومت و خازن (مدار RC) و مدار متشکل از مقاومت و سلف (مدار RL) هستند. در این آموزش، مدار مرتبه اول RC را با جزئیات بررسی خواهیم کرد.. برای اطلاعات بیشتر و مفید روی این لینک کلیک نمایید …
«اختلاف فاز» (Phase Difference)، اختلاف بین دو یا چند کمیت متناوب را بر حسب درجه یا رادیان توضیح میدهد.همانطور که میدانیم، شکل موج سینوسی، یک کمیت متناوب است و میتوان آن را نسبت به محور افقی زمان رسم کرد.: برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
مقاومتهای سری
به اتصال زنجیروار مقاومتها، اتصال سری گفته میشود. در این حالت جریان گذرنده از همه مقاومتها با هم برابر است. مقاومتها میتوانند به صورت سری، متوالی یا سری-متوالی به یکدیگر متصل شوند. به این ترتیب، شبکه مقاومتی حاصل پیچیدهتر میشود و مقاومت معادل آن با محاسبات ریاضی به دست میآید. برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
تقسیم ولتاژ در مدارات سری
در این آموزش، قاعده تقسیم ولتاژ را بیان میکنیم که با استفاده از آن میتوانیم ولتاژ هر مقاومت سری را در یک مرحله و بدون نیاز به محاسبه جریان به دست آوریم. برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
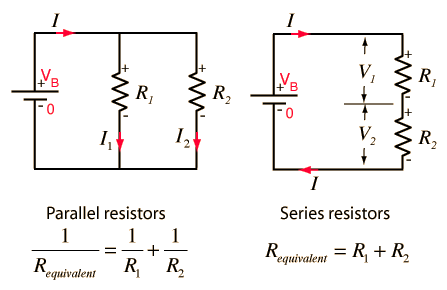
مقاومتهای موازی
در این مطلب مدار موازی را بررسی میکنیم و تغییرات ولتاژ و جریان را در این مدار مورد تجزیه و تحلیل قرار میدهیم. همچنین در مورد مقاومت، خازن و سلف یا القاگر که در یک مدار به صورت موازی متصل شده باشند نیز صحبت خواهیم کرد. برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
مدارات ترکیبی ( سری - موازی )
مدارات سری – موازی به عنوان مدارهای ترکیبی یا مختلط نیز بیان میشوند .
قوانین KVL & KCL در مدارات الکتریکی
گاهی، استفاده از قانون اهم برای به دست آوردن ولتاژ و جریان مدارهای پیچیده، دشوار است. در نتیجه، برای انجام محاسبات مربوط به این مدارها به قوانینی نیاز داریم که بتوانیم بر اساس آن، معادلات مدار را به دست آوریم. قانون مداری کیرشهف، یکی از راهحلهای مناسب برای این کار است . برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
آموزش حل مدار از طریق مش یا حلقه
قوانین مداری کیرشهف (KVL و KCL)، ابزار اساسی تحلیل هر مدار پیچیدهای را به ما میدهند، اما راههای دیگری مانند روش تحلیل جریان مش و روش تحلیل ولتاژ گره وجود دارند که ریاضیات و محاسبات تحلیل شبکههای بزرگ را کاهش میدهند. . برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
حل یک مثال ترکیبی از روش جمع آثار و مش
ویدیوی آموزشی زیر در سه قسمت یک مثال کاربردی که در آن قانون جمع آثار و قانون مش ( حلقه ) مورد بررسی قرار میگیرند را به صورت ساده و قابل فهم ارائه داده است .
قانون تونن
در آموزشهای قبل دیدیم که میتوان مدارهای الکتریکی پیچیده را با قوانین مداری کیرشهف (KVL و KCL)، تحلیل مش و تحلیل گره حل کرد. اما علاوه بر این روشها، قضایای تحلیل مداری وجود دارند که با استفاده از آنها میتوان جریان و ولتاژ هر نقطهای از مدار را محاسبه کرد. در این آموزش، «قضیه تونن» (Thevenin’s Theorem) را معرفی میکنیم که یکی از مهمترین قضایای تحلیل مدار است. . برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …
قانون نورتن
«قضیه نورتن» (Nortons Theorem) دوگان قضیه تونن است و بیان میکند: «هر مدار خطی از منابع انرژی و مقاومتها را میتوان به یک منبع جریان موازی با مقاومت کاهش داد». . برای اطلاعات بیشتر و مفید روی این لینک کلیک کنید …



